The Secret to a Happy Dev Life
Apart from some slightly unique user experience flows and some scalability or performance issues here and there, your daily life as a web or app developer is pretty repetitive. After all, there are only so many frameworks you can learn, and, let’s be honest, exchanging data and tasks between a server and a client is not really that complicated.
I think it’s safe to say that creativity or real problem solving are actually not that common in day-to-day software development, and this can quickly lead to a dull / boring life.
But coding can be much more than that so I recently decided to spend a bit more time working on things that actually bring me joy. In other words, I’m planning to spend less time building UIs in any of the random frameworks that just reinvent the wheel or implement REST APIs which perform the same old CRUD operations on a database, and I will spend more time on coding solutions for problems I find interesting.
What’s funny though, is that I’m sure this will make me a better programmer since I’ll be forced to get out of my comfort zone and practice some of the coding skills I didn’t get the chance to use in a long time. Creating a programming language is one of those things that always fascinated me. So I picked up “Writing an Interpreter in Go” and, among all the useful information, I found Bob’s article describing in detail a small algorithm which is so elegant yet simple that it reminded me why I fell in love with coding in the first place.
So today we’ll learn about Pratt Parsers. Don’t worry - I know this sounds boring and complicated but it actually isn’t. Even though the algorithm solves a very specific problem in the process of building a programming language, it is filled with useful lessons which can help you better understand the basics.
The Basics
Let’s start by spending a few moments laying down the technical knowledge needed in this context.
A programming language is a set of human readable instructions which can then be interpreted or compiled to code that machines can execute.This conversion process from human instructions to machine instructions is done in three steps.
- First, the source code is converted into a sequence of tokens.
- Then these tokens are parsed and organized into a special structure called an Abstract Syntax Tree.
- Finally, the AST is evaluated and interpreted or compiled depending on the language.
Of course, there are numerous complex processes under the hood, but from a bird’s-eye view, these are the exact steps.
In practice, an assignment instruction such as this one would first be converted into this simplified tokenized structure. Then these tokens are converted into an abstract syntax tree which will finally be interpreted or compiled.
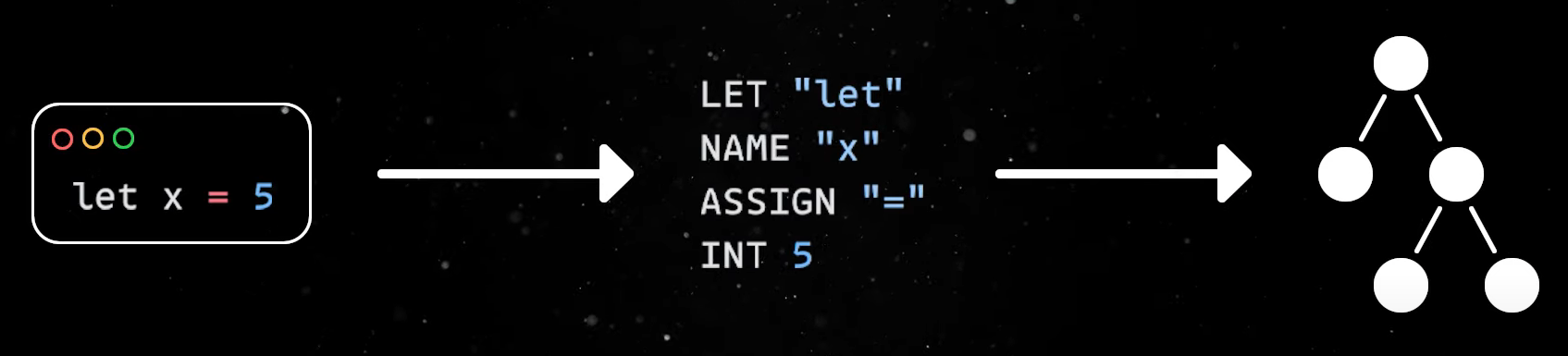
A Pratt parser solves the problem of converting the list of tokens into the tree structure. Of course, there are various use cases and scenarios you have to think about ranging from your usual assignment statement (var x = “Awesome”) to prefix operators (var isLogged = !anonymous) or operator precedence in a mathematical expression (var total = 2 + 4 * (6 - 1)).
All these have to be correctly converted into tree structures that can be traversed and which output the desired result. And this is where the interesting bit comes in. Despite the complexity of software expressions and the sheer number of rules and variations, a Pratt parser solves this in an elegant manner, in just a few lines of code.
It is worth mentioning that our parser is purely an exercise in implementing algorithms. In practice, for production grade languages, you can use generators which create parsers from a formal description of a language. Once generated, these parsers take source code as input and produce highly performant, optimized syntax trees.
Ok, with some of the theory out of the way, let’s write some code.
The implementation
We’ll write our parser in Kotlin, since we don’t have any performance constraints, so we can enjoy an expressive syntax with a fun developer experience.
Remember that our parser is an intermediate step between source code and machine code, which consumes a list of tokens provided by a lexer and returns a tree structure.
Let’s quickly look at the Lexer implementation just to give you an idea about what that looks like. Again, once you really think about it, there is nothing crazy difficult in here. The lexer receives the raw input and exposes a next() function which traverses the input character by character and converts it into a Token entity. We make a difference between punctuators which are usually one character operators, and other letters which are usually variable names or reserved keywords.
// Lexer.kt
fun next(): Token {
while (idx < input.length) {
val char = input[idx++]
if (PUNCTUATORS.containsKey(char)) {
return Token(PUNCTUATORS[char]!!, char.toString())
} else if (Character.isLetter(char)) {
val start = idx - 1
while (idx < input.length) {
if (!Character.isLetter(input[idx])) break
idx++
}
val name = input.substring(start, idx)
return Token(TokenType.NAME, name)
}
}
return Token(TokenType.EOF, "")
}
The Token entity is simply grouping a token type and the actual value under the same object.
// Token.kt
enum class TokenType(val value: Char?) {
LEFT_PAREN('('),
RIGHT_PAREN(')'),
COMMA(','),
ASSIGN('='),
PLUS('+'),
MINUS('-'),
ASTERISK('*'),
NAME(null),
EOF(null);
}
class Token(
val type: TokenType,
val value: String
)
Ok, now let’s look at the parser which keeps track of a lexer reference and exposes a parse expression function where all the magic happens.
class Parser(
val lexer: Lexer
) {
fun parseExpression(): Expression {
}
}
The easiest expressions to parse are prefix operators like the minus sign before an integer or a bang sign to negate a boolean and single-token expressions such as variable names.
So once we consume a token, we can simply check the token type and convert the token into either a NamedExpression or a PrefixExpression, which are very simple, straight forward structures.
class NameExpression(
val name: String
)
class PrefixExpression(
val operator: TokenType,
val right: Expression
)
Or, better yet, since we might want to extend our parser later with more prefix operators or single-token expressions we could store all these in a map structure with the Token Types as keys and the Parse strategy as value.
class Parser(
val lexer: Lexer,
val tokenBuffer: MutableList<Token> = mutableListOf(),
var prefixParsers: MutableMap<TokenType, PrefixParser> = mutableMapOf(),
) {
init {
prefixParsers[TokenType.NAME] = NameParser()
prefixParsers[TokenType.PLUS] = PrefixOperatorParser()
prefixParsers[TokenType.MINUS] = PrefixOperatorParser()
}
fun parseExpression(): Expression {}
}
Now we can fetch the correct parser, through an exception if we found a token we don’t know how to parse, and then simply obtain the result.
class Parser(
val lexer: Lexer,
val tokenBuffer: MutableList<Token> = mutableListOf(),
var prefixParsers: MutableMap<TokenType, PrefixParser> = mutableMapOf(),
) {
init {
prefixParsers[TokenType.NAME] = NameParser()
prefixParsers[TokenType.PLUS] = PrefixOperatorParser()
prefixParsers[TokenType.MINUS] = PrefixOperatorParser()
}
fun parseExpression(): Expression {
var token = consume()
val prefixParser = prefixParsers[token.type] ?: throw Exception()
return prefixParser.parse(this, token)
}
}
Now let’s look at the parse strategy for these types of expressions.
The name parser is very straight forward. It simply returns an object containing the token value.
class NameParser {
fun parse(parser: Parser, token: Token): Expression {
return NameExpression(token.value)
}
}
The prefix parser is a bit more interesting because besides the actual token type, which can be the minus sign or the bang operator, it also contains an evaluation of the right hand side of the expression. Here is where the fun begins since this is a recursive call to the parse expression function.
class PrefixOperatorParser {
fun parse(parser: Parser, token: Token): Expression {
val right = parser.parseExpression()
return PrefixExpression(token.type, right)
}
}
So, in a practical example ( - foo + bar * bux - tor), this expression starts with the minus sign which is a prefix operator. The parser converts this into an expression containing the minus token and then calls parse again. Now, we are back in the parser where a new token is consumed.
“Foo” is a name, so it is going to simply return the name. So, in the end, the Prefix Expression will be a tree node containing the minus sign and the foo name.
Once the prefix parser is completed, the execution returns to the first call of parse expression, and the method simply returns the Prefix Expression. But what about the rest of our expression? Clearly we need to parse it as well.
We see that the plus sign is the following token, and this is a binary operator which takes two values or expressions and combines them to produce a result.
class BinaryOperatorParser(
private val precedence: Int
){
fun parse(parser: Parser, left: Expression, token: Token): Expression {
val right = parser.parseExpression(precedence)
return OperatorExpression(left, token.type, right)
}
}
So an operator expression will have left and right expressions and the actual operator stored as a token type.
The operator parser receives the already evaluated left hand side expression, and uses recursion to parse the right side as well.
So back in our parser we’ll first define a map to store parser for infix operators, and register our Operator Parser for the token types we want to be able to convert.
class Parser(
val lexer: Lexer,
val tokenBuffer: MutableList<Token> = mutableListOf(),
var prefixParsers: MutableMap<TokenType, PrefixParser> = mutableMapOf(),
var infixParsers: MutableMap<TokenType, InfixParser> = mutableMapOf()
) {
init {
prefixParsers[TokenType.NAME] = NameParser()
prefixParsers[TokenType.PLUS] = PrefixOperatorParser()
prefixParsers[TokenType.MINUS] = PrefixOperatorParser()
infixParsers[TokenType.PLUS] = BinaryOperatorParser()
infixParsers[TokenType.MINUS] = BinaryOperatorParser()
infixParsers[TokenType.ASTERISK] = BinaryOperatorParser()
}
}
Then, in the parse expression function, we’ll make some small adjustments. The initial prefix parse result will become the left hand side of our expression, and then we’ll consume a new token, fetch the appropriate infix parser and perform the parsing again.
fun parseExpression(): Expression {
var token = consume()
val prefixParser = prefixParsers[token.type] ?: throw Exception()
var expression = prefixParser.parse(this, token)
token = consume()
val infixParser = infixParsers[token.type] ?: return expression
return infixParser.parse(this, expression, token)
}
This is it - now we can evaluate basic expressions.
So if we follow our implementation step by step, you’ll see that our parse method traverses all tokens first, and then builds the appropriate expressions from right to left. There is one major flaw here - there is no operator precedence. In practice the product of two numbers should be evaluated before sums and differences.
We can solve this in a very easy manner. We’ll first define an enum class, where precedences are declared in order from the least important to the most important.
enum class Precedence(val value: Int) {
ASSIGNMENT(1),
CONDITIONAL(2),
SUM(3),
PRODUCT(4),
EXPONENT(5),
PREFIX(6),
POSTFIX(7),
CALL(8)
}
Then, each of our parsers will receive its own precedence value.
init {
prefixParsers[TokenType.NAME] = NameParser()
prefixParsers[TokenType.PLUS] = PrefixOperatorParser(Precedence.SUM.value)
prefixParsers[TokenType.MINUS] = PrefixOperatorParser(Precedence.SUM.value)
infixParsers[TokenType.PLUS] = BinaryOperatorParser(Precedence.SUM.value)
infixParsers[TokenType.MINUS] = BinaryOperatorParser(Precedence.SUM.value)
infixParsers[TokenType.ASTERISK] = BinaryOperatorParser(Precedence.PRODUCT.value)
}
Finally, in the parse expression function, we’ll evaluate the right hand side of an expression only if the current parser precedence is lower than the precedence of the parser associated with the next token.
fun parseExpression(precedence: Int = 0): Expression {
var token = consume()
val prefixParser = prefixParsers[token.type] ?: throw Exception()
var expression = prefixParser.parse(this, token)
val nextPrecedence = nextPrecedence()
while (precedence < nextPrecedence) {
token = consume()
val infixParser = infixParsers[token.type] ?: return expression
expression = infixParser.parse(this, expression, token)
}
return expression
}
Now our expressions are correctly evaluated!
Note that all we built here is the grown work needed to create a full fledged parser. All the concepts we discussed can be used to extrapolate to more complex expressions, operators and precedence rules.
So here is my secret to a happy dev life after 15 years of grind. Always spend time learning new things and working on problems that interest you. It can be a full product or a simple algorithm. You’ll grow as a developer and have fun along the way.
If you feel like you learned something, you should watch some of my youtube videos or subscribe to the newsletter.
Until next time, thank you for reading!